By Dr. Sam L. Savage
The Bootstrap
Brad Efron, an acclaimed statistician, is most famous for his bootstrap resampling technique, which helped usher in the era of computational statistics in the late 1970s. Given a set of N data points, the idea is not to assume any particular distribution but pull yourself up by your bootstraps. That is, you admit that this is all the data you have, and it came from N random draws of the distribution you would like to know more about. And you say, “what would other random draws of N look like?” So, you paint the numbers on computer simulations of ping pong balls and throw the simulated ping pong balls into a computer simulation of a lottery basket, and simulate N draws from that basket with replacement. Do that thousands of times and see what you get. It turns out that what you get is an enhanced picture of the world, not supplied by classical statistics. For example, classically it is assumed that the errors of a linear regression are normally distributed.
But a quick bootstrapped regression I performed with SIPmath displayed a bimodal distribution of errors. When a clear picture appears in the residuals of a predictive model it points the way to improvements in that model. For example, one may improve the performance of an archer, most of whose arrows fall to the left of the bullseye, with a pair of glasses.
The Arithmetic of Uncertainty and Brad’s Paradox Dice
Computational Statistics is based on simulations. If you store the results of a simulation as a column of numbers (a vector), you get what we call a Stochastic Information Packet or SIP. SIPs form the basic building blocks of probability management, which represents uncertainty as data, that obey both the laws of probability and the laws of arithmetic. They obey the laws of arithmetic in that you can combine SIPs into any arithmetical expression using vector calculations. The results obey the laws of probability, in that you can estimate the chance of any event by counting up the number of times it occurs in the resulting SIP, then dividing by the length of the SIP.
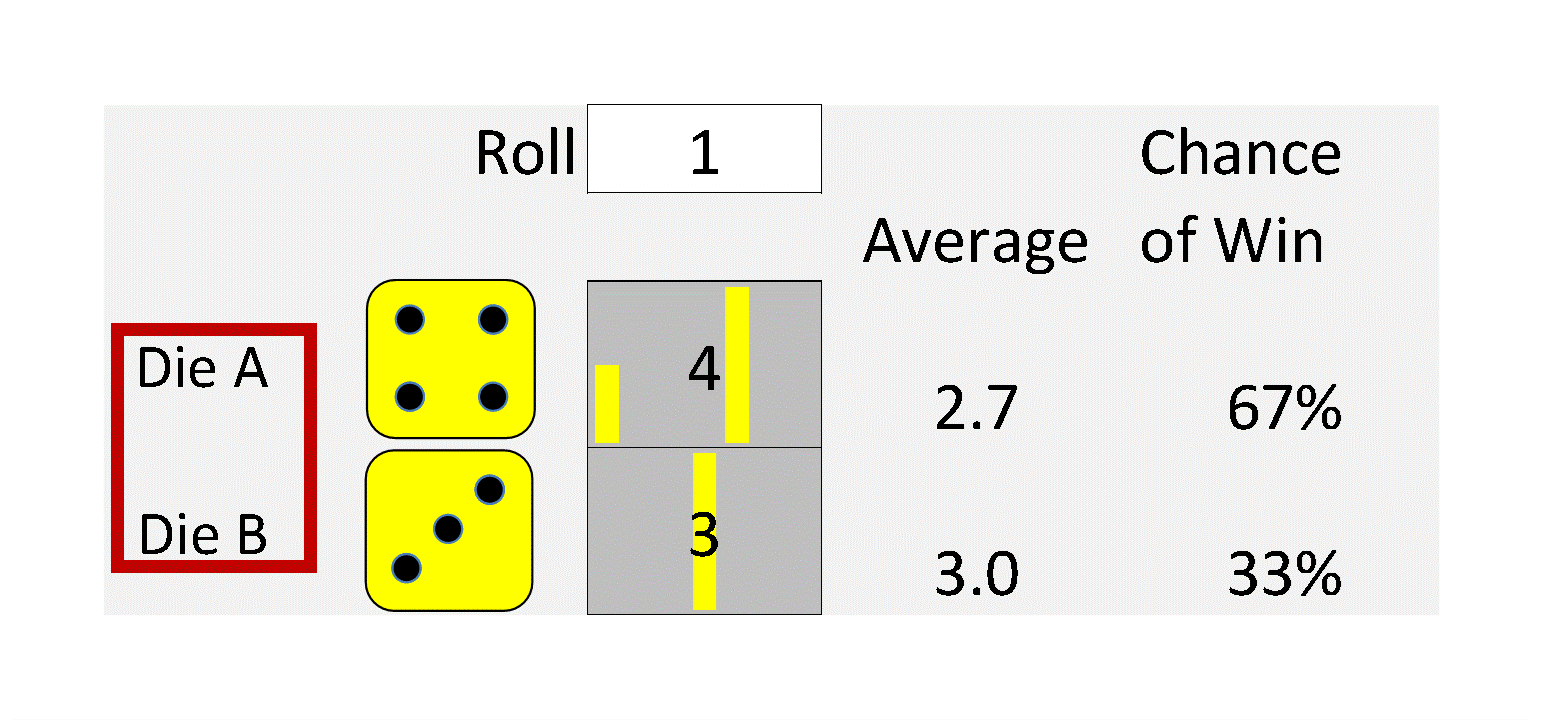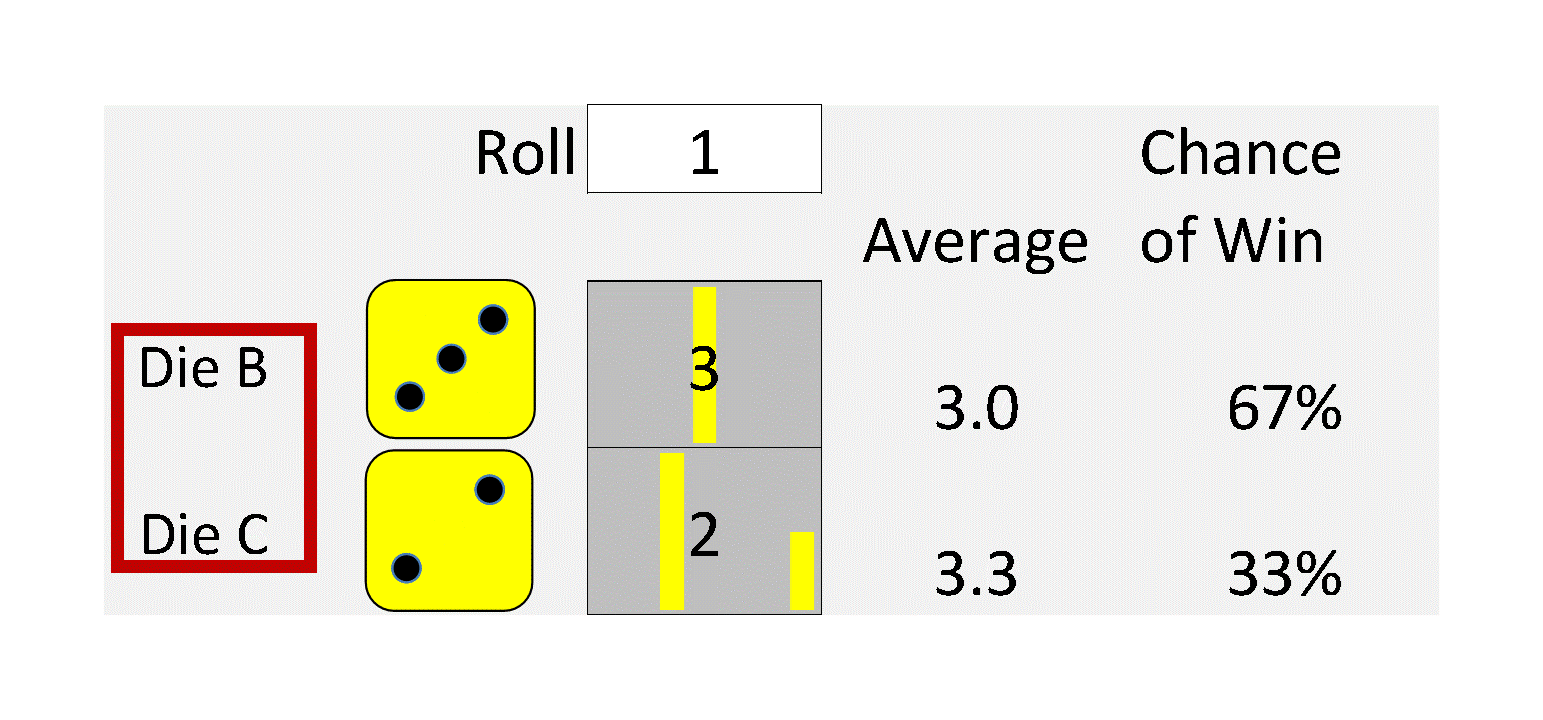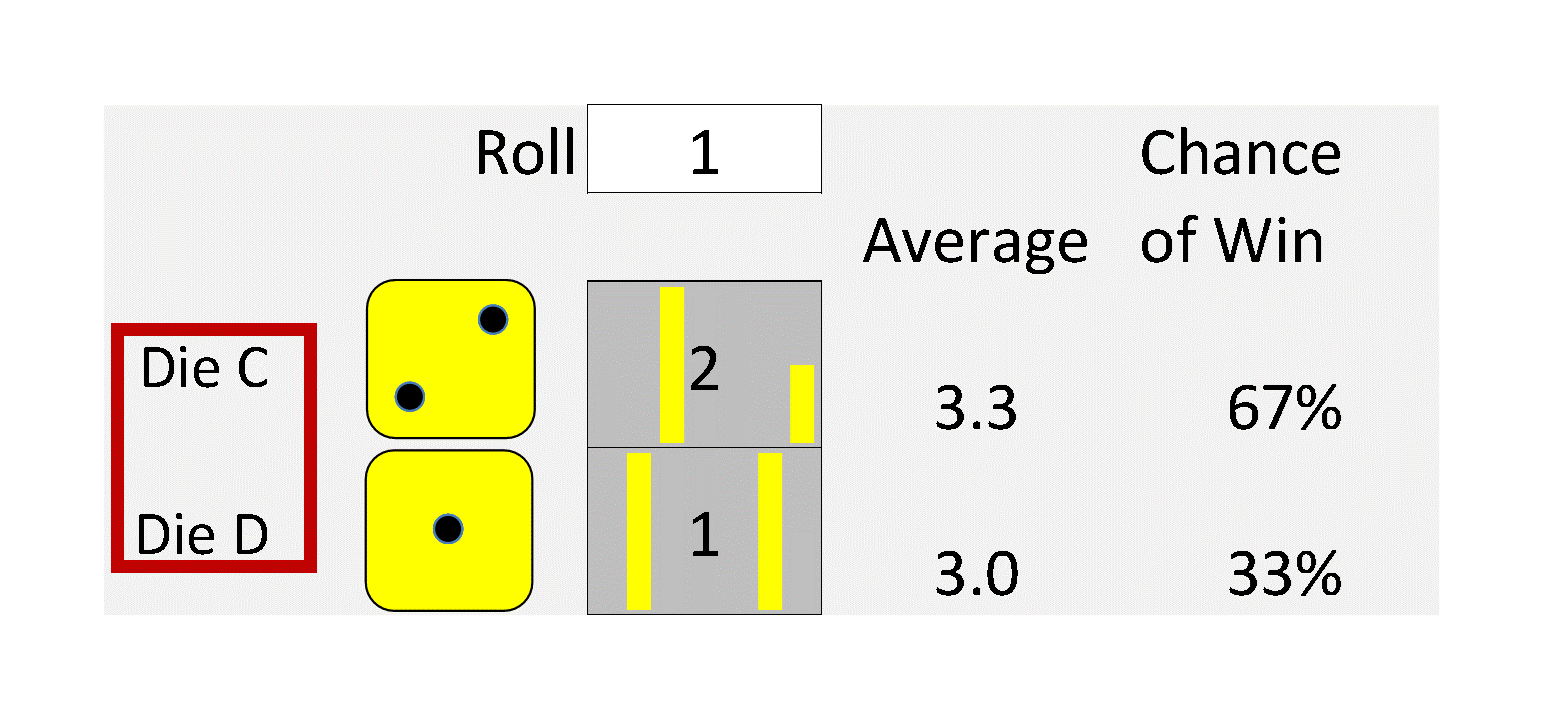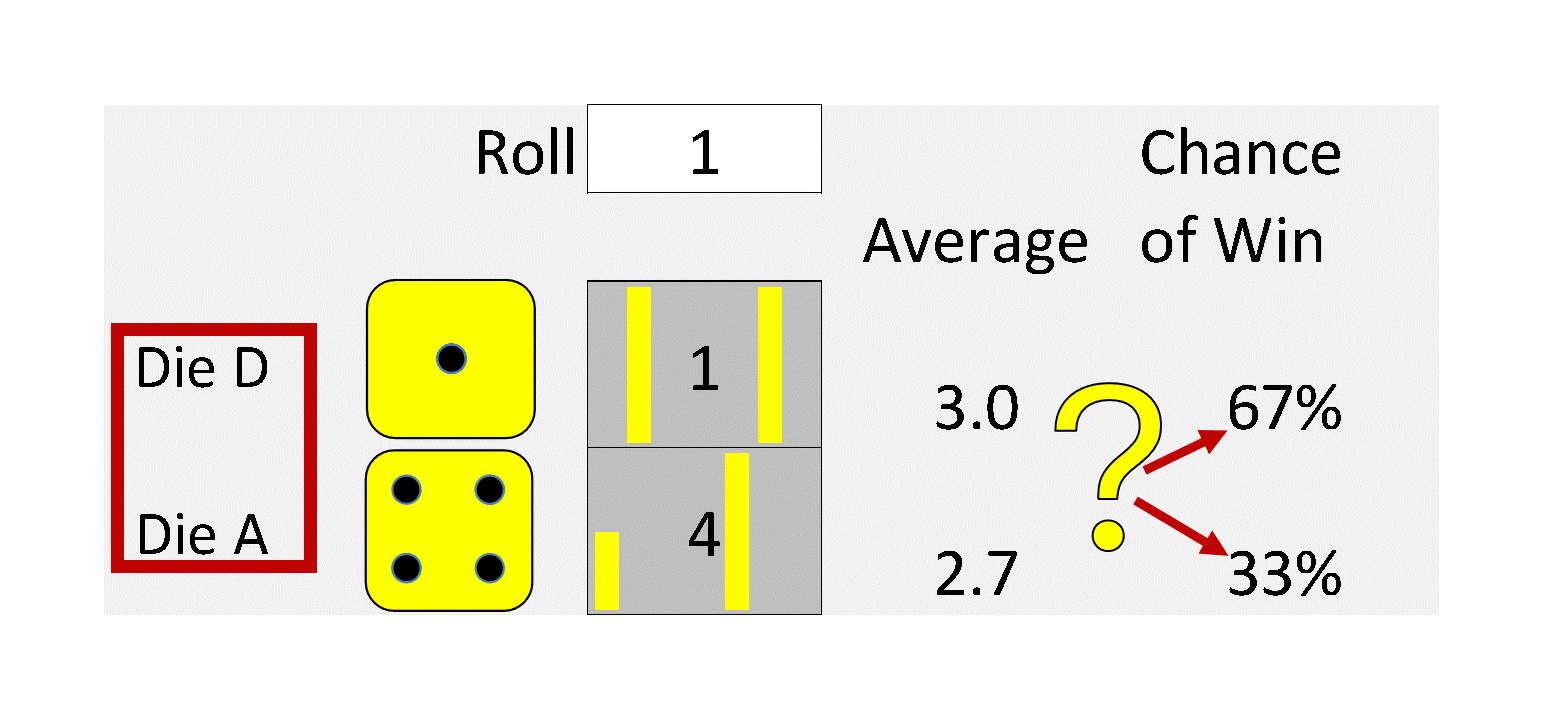
This is useful because the arithmetic of uncertainty can be wildly unintuitive. Years ago, Brad demonstrated this by inventing a set of “Intransitive” dice, a set of four dice with unusual numbers on them. When played against each other, on average, Die A beats Die B. Die B beats die C, Die C beats Die D. And wait for it … Die D beats die A!
I wish we could, but no luck! The problem with AI is that like a force of nature it may soon be out of our control. However, we can at least take steps to protect ourselves. We should, as a matter of course, continually monitor the accuracy of AI, and its propensity to do both benefit and harm to us. Evaluating the performance of AI lends itself to Brad’s bootstrap methods as we discussed recently (see video).
Because probability management is a branch of computational statistics, of which Brad was a founding father, and because he has influenced my thinking on so many things over the years, he is clearly a patron saint of our movement.
Copyright © 2025 Sam L. Savage