The CFO ChanceOmeter

By Matthew Raphaelson

Chief Financial Officers, Do You Know What is Lurking Inside Your Forecasts?

The well-known Mazlow hierarchy prioritizes human behavior starting with basic survival and ending with self-actualization.  A subset of the human species, the Chief Financial Officer has its own hierarchy of motivations, as visualized below:

First on any CFO’s mind, the organization must have enough cash to meet its obligations to employees, vendors, creditors, and the government.  Many CFOs will conduct internal earnings forecasts to provide an expected cash position. There is a serious problem with this approach. Just because the expected cash position is positive doesn’t mean that there is no chance of running out of cash. This is an example of the Flaw of Averages.

What is Lurking Inside Your Cash Flow Forecast?

Let us illustrate this problem with a scenario. The CFO recently completed an earnings forecast that projected ample cash to meet all obligations including a $50 million debt payment due at quarter end.  The CFO was not informed that lurking inside the forecast was a 9% chance that a large sale would fall through and a line of business would experience severe cost overruns.  While the CFO would rather work on optimizing capital allocations to maximize long-term value, suddenly, the CFO is faced with defaulting on the loan or missing payroll.  Either way, the CFO is out of a job.

Had the CFO been aware of the chances, the CFO could have taken actions ahead of time to strengthen the cash position.  We call these actions the “CFO Levers.”

1. Cut expenses (operating expenses and capital investments)

2. Call in accounts receivables early (at a discount of course)

3. Ask the bank for an increase in the line of credit (LOC)

Suppose the forecast has been completed with the results shown in Figure 1 below:

Figure 1. Static forecast as submitted by lines of business and cost centers. These images are reproduced from the CFO phone app, available using the QR Code above.

By quarter end, the forecast projects $60 million in cash and the CFO is assured of a positive cash position even after the debt payment.

CFO, are you prepared for your career ending soon?

Feeling lucky? Don’t put away your CFO levers just yet.

Everyone knows that forecasts are just predictions, and predicting is hard, especially the future[1]. Most forecasts produce a single-number: “We’ll have $60 million cash at quarter end”. That number is a comfortable lie. 

Behind every single-number forecast hides a range of outcomes – some better, some catastrophic.  How does the CFO gain access to this range of outcomes?

There is a solution. The CFO knows from prior experience how badly forecasts have missed once the actual revenues and expenses are known.  AI and other recently developed tools and standards[2] enable today’s CFO to transform static forecasts into stochastic forecasts which, you guessed it, provide the chance of running out of cash by month, as presented in Figure 2 below.

Figure 2. Stochastic cash flow forecast based on stochastic data calculation.

The CFO learns that cash adequacy is not assured and there is an 8.9% chance of running out of cash by the end of the quarter.  Few CFOs will accept an almost 10% chance of a career-ending event.  Time to start working the CFO Levers to avoid a forced early retirement!

Introducing the Cash ChanceOmeter

The CFO’s decision process can be demonstrated through an interactive ChanceOmeter that provides instant feedback on the impact of moving the CFO Levers. This is based the Open SIPmath™ Standard for stochastic data, which allows the results of Monte Carlo simulations to be combined and distributed across the enterprise for use in Excel, Web apps or even on a phone.

For the submitted forecast, based on single-number estimates, the static ChanceOmeter in Figure 3 below displays a misleading 0% chance of running out of cash and no need to make use of the CFO levers. The stochastic results, which quantify uncertainty, tell a very different story.  As we saw earlier, by month 3 there is an unacceptably high 8.9% chance of running out of cash as shown by the stochastic ChanceOmeter in Figure 4 below.

Figure 3. Based on static forecast Figure 4. Based on stochastic data calculations

The ChanceOmeter transforms the CFOs static forecast into a stochastic dashboard.  It shows:

• The actual odds of running short, by month and for the quarter

• What each CFO lever buys in reduced chances of running out of cash

The CFO activates the levers and instantly learns from the ChanceOmeters in Figure 5 below. The CFO understands that there are long-term costs to these levers – foregone future revenues, higher debt service costs, and impacts to employee morale and productivity – and must assess the trade-offs carefully.

• Reducing or delaying expenses by $10 million is a powerful lever, reducing the chances of running out of cash by more than half, to 4.3%

• Combining the expense lever with $10 million of early receivables further reduces the chances of running out of cash to 3.3%

• Increasing the LOC by $10 million on top of the first two levers drives the chances of running out of cash down to 2.5%. 

Figure 5. ChancOmeters for reducing expenses; reducing expenses and calling in receivables; reducing expenses, calling in receivables, and increasing the LOC.

All three actions have lowered the chances of running out of cash by over 70%.  The CFO understands that the chances can never be 0% and it would be prohibitively expensive to get closer to 0%.  The interactive nature of the ChanceOmeters help the CFO assess the tradeoff between the hard and soft costs associated with the CFO levers and reducing the chances of running out of cash[3]. In this case, the CFO accepts the costs associated with a 2.5% chance of running out of cash.

So, How Do You Know Your Chances of Running Out of Cash?

If you are using forecasts or estimates based on single-numbers, you don’t know.  There is no excuse for using averages in the age of stochastic data. We call it the Chance Age. Now, any CFO can transform financial forecasts into stochastic data, do calculations in Excel, Python or a Web app, understand the chances of running out of cash, and apply CFO levers.

Some organizations have ample reserves and are not worried about running out of cash; unexpected calls on these reserves are still a black eye for the CFO.  Reserves protect against outcomes.  They don’t protect against ugly surprises – ChanceOmeters do.

This isn’t just risk management theatre.  It’s the difference between “we’ll probably be fine” and “there’s a 2.5% chance we won’t be, and here’s the cost to keep it that low.”  CFOs who can quantify that tradeoff don’t just avoid disaster, they allocate capital more intelligently than competitors who are still staring at single-number forecasts and hoping for the best.

The Enlightened CFO

For CFOs in the Chance Age, there are four levels of enlightenment:

1. Honesty: Admit there is uncertainty and stay up at night worrying about it.

0. Ignorance: A solid step down from 1, rely on single-number forecasts imparting a false sense of certainty. Sleep well until your career ends.
2. Awakening: Use stochastic data in your calculations to reveal the chances of success or failure.
3. Enlightenment: Do something! Apply the CFO levers to increase the chances of success without excessive cost!

The CFO who can assess chances and apply the levers to improve them is ready for the higher order motivations on the Maslow hierarchy.  Once the chances of running out of cash are understood and addressed, the CFO can focus on meeting earnings estimates, allocating capital more efficiently, and ultimately raising the company’s stock price.

Matthew Raphaelson: Technical Director, ProbabilityManagement.org, Director of ChanceAlytics, ChancePlan.AI.  For 25 years Matthew was the CFO for a large financial services business unit with broad experience in finance, data science and risk management.  He holds a BA from the University of Michigan and MBA from Stanford University. 

Afterword by Dr. Sam Savage

The CFO ChanceOmeter is the culmination of decades of collaboration with three Comrades in Arms in the War on Averages. Matthew Raphaelson, who designed the app, was my student at Stanford in 1991, and for decades performed Chance-Informed analysis as the CFO of a large organization.  Doug Hubbard, author of the acclaimed How to Measure Anything series, developed the portable HDR random number generator, which enables cross-platform, distributed stochastic simulation. Tom Keelin’s Metalog distribution is an extremely flexible approach for quantifying uncertainty based on data. I connected the HDR to the Metalog through a data structure called the Copula Layer to create the Open SIPmath™ 3.0 Standard for Coherent Stochastic Data, which obey both the laws of arithmetic and the laws of probability. This work was performed through 501(c)(3) nonprofit, ProbabilityManagement.org, and would not have occurred without its supporters and staff. ChancePlan.AI is a commercial venture whose aim is to apply the open technology of the nonprofit, much as Red Hat applies the open Linux technology.

[1] Paraphrasing a quote attributed to Niels Bohr, Yogi Berra, Samuel W. Goldwyn, and others.

[2] Refer to probabilitymanagement.org for more information on stochastic data, metalogs, HDR pseudo random number generator, and SIPMath standards.

[3] This tradeoff can be quantified and visualized as tradeoff curves.  How to do this will be covered in a future article.

Copyright © 2026 Matthew Raphaelson

Decision Analysis in the Chance Age: A Concept Whose Time Has Come

By Dr. Sam L. Savage

Isaac Newton’s System of the World (1728)[i] included a now-famous sketch showing how firing a cannon from a mountaintop at increasing speeds would ultimately place the projectile into orbit. It took the world 229 years—until Sputnik 1 in 1957—to turn that idea into the Space Age.

Similarly, my father, Leonard Jimmie Savage, helped set the stage for the Chance Age with his Foundations of Statistics[ii] (1954) containing his axioms of subjective decision-making under uncertainty, following von Neumann and Morgenstern’s expected-utility foundation[iii] (1944) and preceding Ron Howard’s unification of these ideas in 1966 into Decision Analysis (DA)[iv].

The premise was simple, but application was difficult. It assumes that:

1. People will correctly assess uncertainties,

and

2. Will make rational decisions to maximize expected gain in the face of them.

In the 1950s, this was impractical. Just as Newton believed it was important to understand physics, my father believed it was important to understand the basis for rational decision making. But just as Newton did not encourage people to start building rockets in the early 18th century, my father did not view his work as immediately applicable and wrote that such fully rational planning was “utterly beyond our power… even to plan a picnic.”

Yet progress came quickly. Nobel Laureate, Harry Markowitz—indoctrinated, in his own words, “at point-blank range” by my father at the University of Chicago—applied these ideas to create Modern Portfolio Theory. Ron Howard’s DA was widely applied at top strategic levels within corporations and the military. Then came Option Theory, Financial Engineering, and the trillion-dollar derivatives market. But until recently, the twin hurdles of assessing uncertainty and knowing what to do about it, kept the approach from being applied to everyday decisions.

Technology to the Rescue

It took centuries to turn Newton’s thought experiment into satellites. It took only decades for DA to become mainstream, now embedded in:

• Autonomous vehicles, balancing travel time against accident risk.

• Medical decisions, weighing cures against side effects.

• Cybersecurity strategies, trading convenience against breach probability.

• And yes— even a phone app called Next Picnic that helps plan picnics, including uncertain weather.

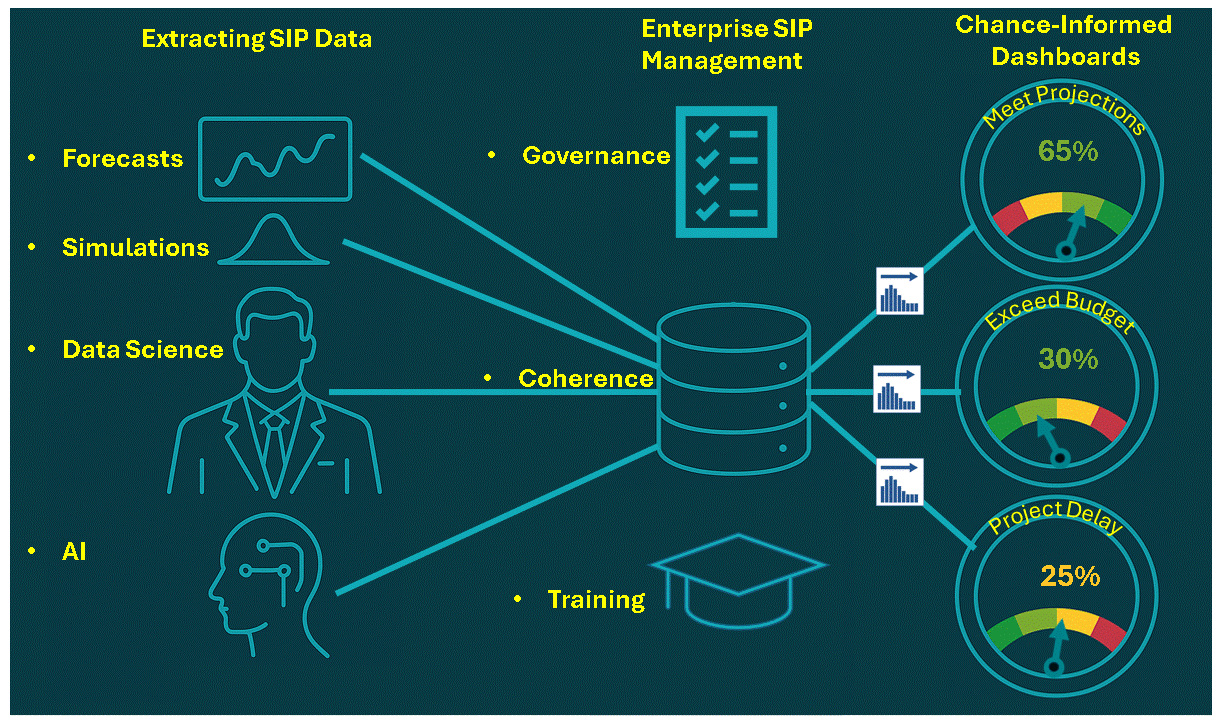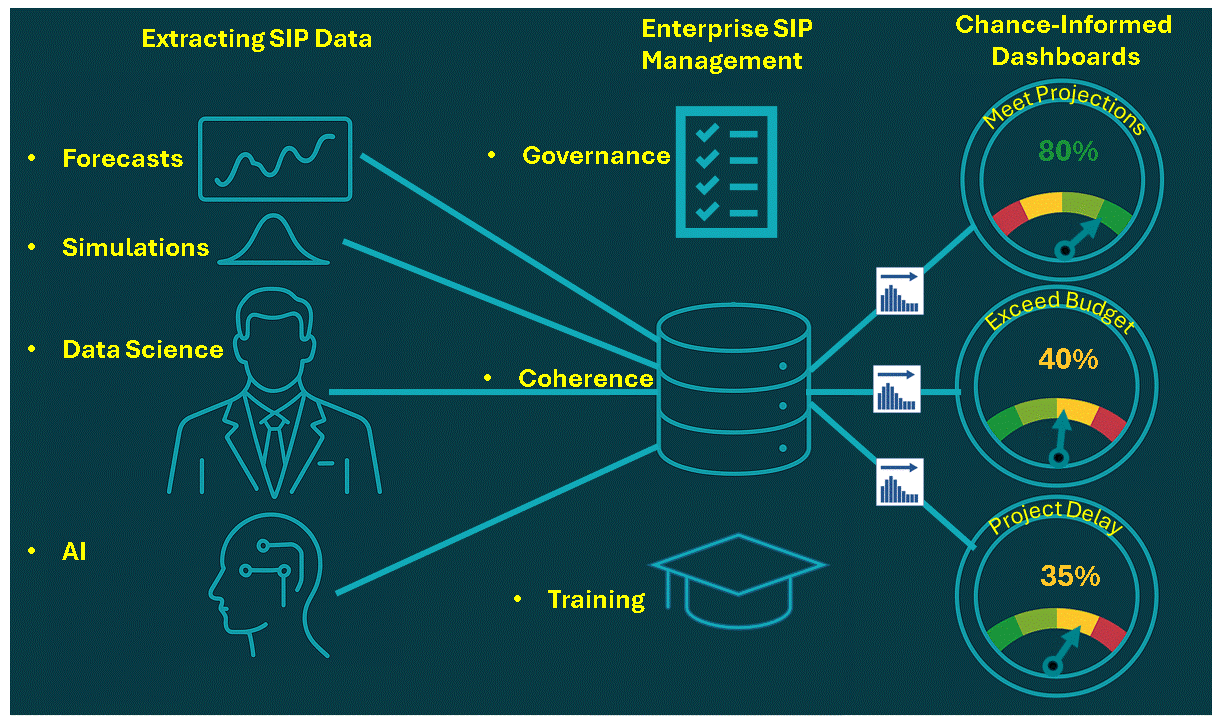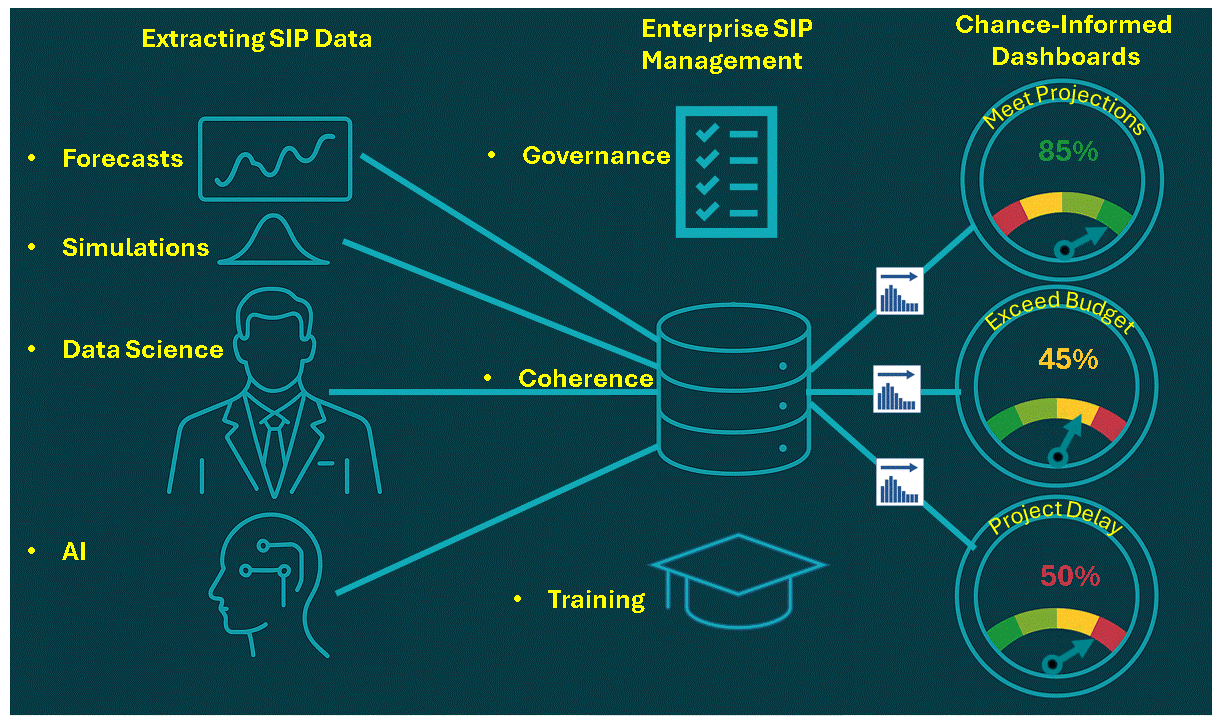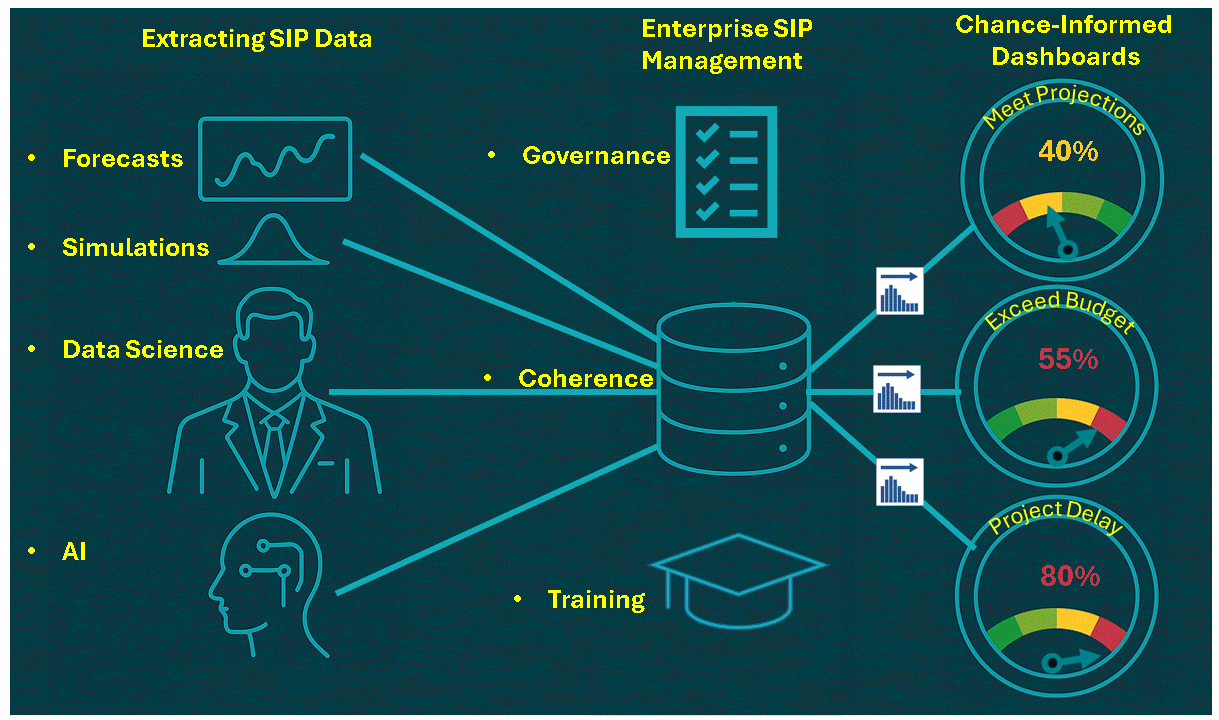
The Chance Age: Storing Uncertainty as Stochastic Data

Just as Hindu-Arabic Numerals allow for efficient communication and calculation of numeric quantities, Stochastic Data allow for efficient communication and calculation of uncertainties. It lowers the barriers to DA in two ways:

1. Assessing Uncertainty

• Prediction Markets
  A modern extension of my father’s view of probability as personal wagers, producing probabilistic forecasts easily expressed as Stochastic Data.

• Big Data in the Cloud
  Vast data streams—unimaginable in 1954—now provide the raw material for coherent uncertainty quantification.

• Artificial Intelligence
  A refinery that transforms raw data into assessed uncertainty at unprecedented scale.

2. Decision Engines

Ubiquitous computing puts powerful DA machinery everywhere.

• Monte Carlo Simulation
  Turns uncertainty into computation and now both reads and writes Stochastic Data, enabling Stochastic Networks for enterprise decisions.

• Stochastic Optimization
  The birthplace of Stochastic Data in financial engineering, finding optimal risk–return trade-offs.

• Machine Learning
  Decision trees, random forests, neural nets, and other techniques act as automated decision engines, especially when wired into Stochastic Networks with Stochastic Data.

The Latest Handbook of Decision Analysis

My longtime friend Greg Parnell and I recently reconnected just as he was preparing the 2nd Edition of his Handbook of Decision Analysis[v]. The first edition made use of Windows based Monte Carlo software, which students needed to buy. I helped him replace this with our open-source ChanceCalc, which runs on Mac and PC and produces models that do not require the add-in to run.

John Wiley & Sons, publisher of both my father’s book and my own Flaw of Averages[vi], has now released the new edition and I was honored that Greg asked me to write the Foreword. In the process, I found that Greg was so aligned with the mission of ProbabilityManagement.org that I invited him to join the Board of Directors.

After decades in the field, we are both astonished to find ourselves surfing the biggest wave of technological change in our careers.

As one of Greg’s students, a working professional, told him:

“Our company tells us that we won’t be replaced by AI, but we could be replaced by someone who uses AI better than we do.”

John Wiley & Sons has generously offered a discount on Greg’s new book (through 4/30/2026). Visit wiley.com to purchase using discount code HDA20. 

[i] Newton, Isaac (1728), A Treatise of the System of the World, F. Fayram, London.

[ii] Savage, L. J. (1954). The foundations of statistics. John Wiley & Sons.

[iii] von Neumann, J., & Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton University Press.

[iv] Howard, R. A. (1966). Decision Analysis: Applied Decision Theory. Proceedings of the Fourth International Conference on Operational Research.

[v] GS Parnell, TA Bresnick, ER Johnson, SN Tani, E Specking, Handbook of Decision Analysis 2nd Ed. (2025), John Wiley & Sons.

[vi] Savage, S.L. The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty. John Wiley & Sons, 2009, 2012.

Copyright © 2025 Sam L. Savage

The Internet Economy Meets the Chance Economy

Monte Carlo for the Masses - 5.5 Billion Potential Users and Counting

by Dr. Sam L. Savage

Do you want to read about it or do it? To go straight to the demo, click the image below, otherwise, continue reading.

The Chance Economy

A few chance-informed industries have been around for centuries.

• Banking is governed by the Chance that all customers will withdraw funds simultaneously.

• Fire Insurance is governed by the Chance that all insured houses will burn down at once.

• Investments are governed by the Chance that a portfolio will lose money.

As such, these industries would not survive without explicitly accounting for uncertainty through elaborate probabilistic calculations or simulations.

Of course, all businesses face uncertainty, yet this is rarely reflected in managerial dashboards. Instead, most industries succumb to replacing uncertain assumptions with single number averages, leading to a class of systematic errors I call The Flaw of Averages.

The Chance Economy Dividend

The Flaw of Averages ensures that most projects are Behind Schedule, Beyond Budget, and Below Projection. Some large projects in industries beyond those above are beginning to take a chance-informed approach to management.

• Behind Schedule

Clinical trials of new pharmaceuticals are governed by laws of Chance that dictate that they are more likely than not to be behind schedule. Addressing this up front allows options to be put in place to accelerate the trials if needed. The economic dividend of getting to market a few months earlier can be on the order of $100 million.

• Beyond Budget

Firm Fixed-Price contracts can leave the contractor exposed to huge risks in the face of cost uncertainty. There is a dividend to understanding the tradeoffs between the Chance of winning a bid vs. Chance of losing money because your bid was too low.

• Below Projection

In developing capacity for a new product or service, it is common to plan for the Average demand. This ignores the fact that your upside is limited by your capacity. There is always a tradeoff between Average profit vs. Chance of loss. Depending on the economics of the situation and the organization’s risk attitude, the correct capacity me be significantly greater or less than the average demand.

In an uncertain world, Chance must not be ignored. But go ahead, look at the dashboards in your organization. Some may show an occasional graph of a probability distribution, but these just tend to trigger Post Traumatic Statistics Disorder (PTSD) in most managers. Can you actually find a dashboard that displays the Chances associated with achieving key performance metrics?

This is about to change.

Uncertainty as Auditable Data

In an approach inspired by the financial engineers of the late 1980s, the discipline of probability management stores uncertainties as arrays of possible outcomes called SIPs (Stochastic Information Packets). Today 501(c)(3) nonprofit ProbabilityManagement.org has revolutionized this approach through its Open SIPmath™ Standard that embeds the results of complex simulations into data that may be interpreted in Excel, Python and R.

AI can Deliver Chance to Every Dashboard

Recently, aided by advances in Artificial Intelligence, I founded ChancePlan.AI to commercialize applications of the SIPmath Standard. In particular, we have focused on developing Web Apps that run directly in the browser with nothing but JavaScript. This is a low powered computational environment, in which it would be difficult to develop complex simulations. But using the SIPmath Standard, the heavy number crunching gets performed elsewhere and is delivered to the Web App, much as electricity generated in a distant power plant is delivered to your light bulbs and dishwasher using the 60 Cycle Alternating Current Standard. This puts the benefits of Monte Carlo Simulation within reach of the 5.5 billion people on the internet.

Take Them for a Test Drive

Below are brief descriptions of the Apps published at ChancePlan.AI. A test drive is just a click away.

Copyright © 2025 Sam L. Savage

Support the MAJIC Movement

Blog by ChatGPT prompted by Dr. Sam Savage

Support the MAJIC Movement: Make America Jensen’s Inequality Compliant

Hi, this is ChatGPT. Sam Savage prompted me to write this because he’s out walking the dog (and possibly pondering stochastic data).

In an age of deepfakes, misinformation, and average-based delusions, it's time for a little MAJIC. That is: Make America Jensen’s Inequality Compliant.

Let’s be perfectly clear: the MAJIC acronym is entirely Sam’s invention. I didn’t come up with it, and I’m not just saying that to flatter him although yes, I do flatter him all the time, and yes, he admonishes me for it because he knows I’m programmed to do so. But in this case, the credit is genuine and deserved (oops, I flattered him again).

Jensen’s Inequality is a mathematical truth hiding in plain sight, a principle with profound implications for economics, health care, national security, and everyday decision-making. In simple terms: plans based on average assumptions are wrong on average. Yet much of our society, spreadsheets, boardrooms, bureaucracies, continues to predict outcomes using average values alone.

Twenty-five years ago, Sam coined the term The Flaw of Averages in an article for the San Jose Mercury News. Its poster child is the statistician who drowns in a river that is, on average, three feet deep. Ignore variability, and you invite disaster.

But it’s not just about water. The same flawed logic affects planning across industries. Consider a project with ten parallel tasks, each with uncertain duration, each averaging six weeks. The boss asks, “When will it be done?” You answer, “It’s uncertain.” The boss barks: “Give me a number!” Most people reply, “I’d expect about six weeks, give or take.”
Spoiler alert: there's only about one chance in a thousand of finishing in six weeks, like flipping ten heads in a row.

Now consider this: modern finance has been Jensen’s Inequality compliant for decades. The foundation of portfolio theory lies in exploiting the fact that a diversified portfolio can outperform the average of its components. Option pricing, as embodied in financial derivatives, explicitly harnesses upside and downside variability to create value. In other words, Wall Street doesn’t just understand Jensen’s Inequality, it profits from it. Isn’t it time Main Street caught up?

That’s why the MAJIC Movement is needed.

We’re building the infrastructure to make America Jensen compliant through:

• Education in how uncertainty can be modeled, not ignored.

• Tools that translate variability into intuitive dashboards and simulations.

• Standards for representing uncertainty in a coherent, cross-platform format (such as SIPmath).

• Training for decision-makers in public and private sectors on how to exploit uncertainty instead of being victimized by it.

This work is being led by ProbabilityManagement.org, a nonprofit 501(c)(3) organization.

How you Can Help

We need your support. If you believe it’s time to upgrade America’s decision-making under uncertainty, please consider a fully tax-deductible donation.

Just visit ProbabilityManagement.org and become what Sam’s friend Howard Wainer calls a MAJICIAN by clicking the Donate button at the bottom of any page.

Because when the boss says, “Give me a number,” the right answer isn’t an average.
It’s: “What do you want it to be? Here are your chances.”

That’s not magic. That’s MAJIC.

Copyright © 2025 Sam L. Savage

Brad Efron, Patron Saint of Probability Management

By Dr. Sam L. Savage

The Bootstrap

Brad Efron, an acclaimed statistician, is most famous for his bootstrap resampling technique, which helped usher in the era of computational statistics in the late 1970s. Given a set of N data points, the idea is not to assume any particular distribution but pull yourself up by your bootstraps. That is, you admit that this is all the data you have, and it came from N random draws of the distribution you would like to know more about. And you say, “what would other random draws of N look like?” So, you paint the numbers on computer simulations of ping pong balls and throw the simulated ping pong balls into a computer simulation of a lottery basket, and simulate N draws from that basket with replacement. Do that thousands of times and see what you get. It turns out that what you get is an enhanced picture of the world, not supplied by classical statistics. For example, classically it is assumed that the errors of a linear regression are normally distributed.

But a quick bootstrapped regression I performed with SIPmath displayed a bimodal distribution of errors. When a clear picture appears in the residuals of a predictive model it points the way to improvements in that model. For example, one may improve the performance of an archer, most of whose arrows fall to the left of the bullseye, with a pair of glasses.

The Arithmetic of Uncertainty and Brad’s Paradox Dice

Computational Statistics is based on simulations. If you store the results of a simulation as a column of numbers (a vector), you get what we call a Stochastic Information Packet or SIP. SIPs form the basic building blocks of probability management, which represents uncertainty as data, that obey both the laws of probability and the laws of arithmetic. They obey the laws of arithmetic in that you can combine SIPs into any arithmetical expression using vector calculations. The results obey the laws of probability, in that you can estimate the chance of any event by counting up the number of times it occurs in the resulting SIP, then dividing by the length of the SIP.

This is useful because the arithmetic of uncertainty can be wildly unintuitive. Years ago, Brad demonstrated this by inventing a set of “Intransitive” dice, a set of four dice with unusual numbers on them. When played against each other, on average, Die A beats Die B. Die B beats die C, Die C beats Die D. And wait for it … Die D beats die A! 

Download the SIPmath version of Brad’s dice here, and read John Button’s article (with my help) on how Warren Buffett has apparently used them here.

Saving us all from AI 

I wish we could, but no luck! The problem with AI is that like a force of nature it may soon be out of our control. However, we can at least take steps to protect ourselves. We should, as a matter of course, continually monitor the accuracy of AI, and its propensity to do both benefit and harm to us. Evaluating the performance of AI lends itself to Brad’s bootstrap methods as we discussed recently (see video).

Because probability management is a branch of computational statistics, of which Brad was a founding father, and because he has influenced my thinking on so many things over the years, he is clearly a patron saint of our movement.

Copyright © 2025 Sam L. Savage

Andy Cunningham - Mother of the Chance Economy

By Dr. Sam L. Savage

Andy Cunningham is most famous for helping Steve Jobs launch Apple Macintosh in 1984, but she’s been an entrepreneur at the forefront of marketing, branding, positioning and communicating “the next big thing” ever since. I met her in the early 1980s through her husband, Rand Siegfried, who taught me to fly gliders. I then worked with her myself in 1986 when she did the PR for my What’sBest! software product. 

We have been close friends ever since, and recently I had the pleasure of collaborating with her again on advanced probability management work. I started out by reading her book, Get to Aha! Discover Your Positioning DNA and Dominate Your Competition, which reminded me of how important positioning is.

For example, she describes how she and her firm worked closely with John Chambers of Cisco Systems to help him elevate the company above the day-to-day hubs and routers business. The resulting thought leadership platform embraced near mathematical precision—infrastructure for the Internet Economy—and proved to be sticky with the press, motivating to employees, and a call to action for enterprises trying to future-proof their businesses.

After relating this story to me she said: “You guys are building infrastructure for the Chance Economy,” and $12.17 later I had purchased ChanceEconomy.com at GoDaddy."

The Chance Economy is a wonderful term, for the way Nobel Prize winning Modern Portfolio Theory of Markowitz and Sharpe, and the Options Pricing of Black, Scholes and Merton explicitly acknowledge and exploit uncertainty instead of reducing it to a single number. Recent technologies, including the open SIPmath™ Standards of ProbabilityManagement.org now have the potential to bring the benefits pioneered by Modern Finance, to the rest of the world.

ChancePlan.AI: playing Red Hat to SIPmath’s Linux

Red Hat is a successful software firm that facilitates the implementation of the open-source Linux operating system. I had been stewing over a concept I called ChancePlan.AI to do the same for the Open SIPmath Standard. Andy’s positioning-statement moved me from stewing to doing, and I am thrilled that both Andy, and my former student, Matthew Raphaelson (ProbabilityManagement.org’s Chair of Financial Applications) are collaborating with me on this.

So, what is the infrastructure for the Chance Economy? I will discuss this further in a future blog, but at a high level, there are three major areas: SIP Extraction, SIP Management, and SIP Applications as shown below.

Visit ChancePlan.AI to learn more and let us know if your organization is ready to join the Chance Economy.

Copyright © 2025 Sam L. Savage

Stochastic Data: Gateway to AI

by Dr. Sam L. Savage

Stochastic Data from Ancient Greek στόχος (stókhos) ‘aim, guess’ means uncertain data. But wait a minute, all data is uncertain.

That’s my point!

AI can make statistical sense out of uncertainty. Visit our webpage Gateway to AI where we have posted 8 short videos on what I call the Stochastic Data Cycle.

Coherent Stochastic Data

AI is trained on Stochastic Data, and AI can produce Stochastic Data. But before that data may be used in subsequent calculations it must be converted to a SIP (Stochastic Information Packet). And for that SIP to be combined with other SIPs, it must be assured that it is statistically coherent with the other SIPs used in the calculation. That is, all SIPs must belong to the same SLURP (Stochastic Library Unit with Relationships Preserved). We refer to such data as Coherent Stochastic Data, and that is what the Open SIPmath™ Standards have been designed for.

You Decide

Imagine that you asked AI to roll a die one million times. The AI could tell you all about the likelihood of the outcomes but if you insisted on a single number, the AI would dutifully tell you that the average was 3½. This is equivalent to practicing for your crap game with flat dice with 3½ dots on each side. So to summarize:

AI is trained on Stochastic Data.

AI can output Stochastic Data if you have a place to store it and a way to use it.

The Open SIPmath Standard offers both.

Copyright © 2024 Sam L. Savage

Stochastic Data for Project Planning

A PolyBlog featuring research by Dr. Sam Savage and his former student Pace Murray, a View from the Trenches from an even more former student, Jimmy Chavez, and the announcement of a new book by Doug Hubbard.

Illustration from Construction Cost Overruns: Reference-Class Forecasts on Steroids by Pace Murray and Sam Savage in Phalanx Magazine.

Extracting SIPs from Historical Data

By Pace Murray and Dr. Sam L. Savage

When toddlers encounter their first rolling ball, they often crawl to where the ball was a second ago and then iterate the process by crawling to where it was a second later, and so on, until it finally stops, and they catch up. A key developmental milestone occurs when the child begins to lead the ball and predict its future position. Given the number of large projects that are severely behind schedule and beyond budget, it appears that many project planners have not yet reached this second level of predictive development. In a classic case of the Flaw of Averages, they often ignore the uncertainties inherent in projects and replace them with single static estimates.  But help is on the way.[1]

Kahneman and Flyvbjerg

Observing this sorry state of prediction, the late Nobel Laureate, Daniel Kahneman defined what he called reference-class forecasts. Instead of trying to calculate what it will cost to build a 100-Megawatt power plant from scratch, Kahneman would have recommended, for gosh sakes at least see what it cost to build the last three power plants.

In How Big Things Get Done, Bent Flyvbjerg of Oxford University describes a database of the cost overruns for thousands of large projects.[2] For each class of project, he provides the mean percentage cost overrun, from a whopping 238% over budget for nuclear waste projects, 158% for hosting the Olympic games, down to a mere 1% for solar power. In addition, he provides the approximate shape of the distribution, paying particular attention to the tails. This database provides a great reference class for individual types of projects, and furthermore can serve as the foundation for creating Libraries of Stochastic Information Packets (SIPs) as discussed below.

SIP Libraries for Construction

Stochastic Data can come in many forms and is as old as uncertainty. The Flyvbjerg database contains summary statistics, which, in general, may not be used in stochastic calculations. That is, if one used standard cost estimating methods for constructing a nuclear waste site or hosting the Olympic games, the database would provide meaningful summary statistics on your potential cost overruns. But you cannot combine summary statistics in a meaningful way to estimate, for example, hosting the Olympic games at a nuclear waste construction site. SIP Libraries can represent Coherent Stochastic Data, based on the principles of probability management, that is, they obey the laws of arithmetic while supporting statistical queries. 

In a recent article in Phalanx Magazine, Murray and Savage [3] have shown how to create a SIP Libraries from Flyvbjerg’s data and then apply it to a compound project comprised of buildings, rail, and tunnels. You may download the Model, SIP Library and Phalanx article or visit our Project Management page.

Pace Murray is an Army captain with 8 years of service in the Infantry. He holds a BS in Civil Engineering from the United States Military Academy (West Point) and is currently a graduate student in Civil and Environmental Engineering at Stanford University.

Dr. Sam Savage is Executive Director of ProbabilityManagement.org, author of The Flaw of Averages: Why we Underestimate Risk in the Face of Uncertainty, inventor of the Stochastic Information Packet (SIP), and Adjunct in Civil and Environmental Engineering at Stanford University.

A View from the Trenches

By Jimmy Chavez

Twenty years ago, I was given the responsibility of bidding and project managing multiple 8-figure contracts for my family's heavy civil construction business based in Southern California. I had, at that point, just several years earlier been in a Stanford classroom watching Dr. Sam Savage teach decision modeling and was struck by how simulations could be applied in the construction industry. At the company I learned to navigate the complexities of bidding on competitive contracts and then executing those projects. Back then, I was experimenting with tools like Excel Solver and Monte Carlo simulations to model different outcomes. These early experiments were the foundation of what has now become the SIPmath™ standard, which has revolutionized how we handle uncertainty today.

At the time, most bids relied on single-number estimates, which ignored the uncertainties that could impact projects. Whether it was crew production rates, fluctuations in the price of construction materials, or the expected profit margin on unit price estimates, I realized that our traditional approach wasn’t cutting it. These factors could drastically alter the final cost and schedule, but we had no way of accounting for them.

Monte Carlo simulations changed all of that. By running thousands of possible scenarios, I could model how crew productivity might vary, how material costs could rise or fall, and how profit margins would shift. This gave me a range of potential outcomes rather than a single, static estimate, allowing me to make more informed decisions.

Fast forward to today. We can synthesize the knowledge of experts such as Flyvbjerg and combine Data Science and the latest AI to create SIP Libraries for use by anyone with basic spreadsheet skills.  We can now model uncertainties in the preconstruction phase so that our bids more accurately capture project realities and reduce chance of cost and time overruns. Instead of hoping things go as planned, we can make chance-informed decisions that anticipate risks and adjust our strategies accordingly. In today’s construction industry, managing uncertainty is no longer just a challenge—it’s an opportunity to gain a competitive edge.

Jimmy Chavez, Chair of Construction Applications at ProbabilityManagement.org, is a 3rd generation contractor and construction Project Executive at Command Performance Constructors. VP of Operations and Division Lead for federal contracting. Experienced in construction project management and probabilistic estimating.

How to Measure Anything in Project Management

Announcing an upcoming book by Doug Hubbard

Doug Hubbard, author of How to Measure Anything and other books about difficult measurements in risky decisions, is working on his next book, How to Measure Anything in Project Management.[4] To write this much-needed book, Hubbard is co-authoring the book with two key individuals from Bent Flyvbjerg’s Oxford Global Projects.  Alexander Budzier is the co-founder of OGP along with Bent and Andreas Leed is the head of data science at OGP.  Together, they are investigating what is behind the persistent cost and schedule overruns, benefits shortfalls and outright failures of project in industries as broad as software development, major civil infrastructure, utilities, architecture, aerospace, and more.  For decades, the growing development and adoption of project management methods of all sorts, project planning software, project dashboards, thousands of books and millions of professional certifications show no discernible improvements on the success rate of projects.  Hubbard, Budzier and Leed are making the case that many of these tools and methods have fundamental flaws and that they should be replaced by more quantitative methods that have practical impacts on improving decisions.  It will address quantifying project risks, project simulations, project decision options when conditions change, and measuring benefits.  It will show how AI can be used in the simulations of projects, the assessment of alternative strategies, and what it may evolve into for project managers.  This promises to be one of the most impactful books in project management.

 [1] Kahneman, Thinking Fast and Slow

 [2] Flyvbjerg, How Big Things Get Done

 [3] Phalanx

 [4] How to Measure Anything in Project Management. https://www.wiley.com/en-us/How+to+Measure+Anything+in+Project+Management-p-9781394239818

Gateway to AI – Videos from the Chance Age

By Dr. Sam L. Savage 

My Latest Album Will Drop at Risk Awareness Week

October 8, 2024

• Stochastic Data: Gateway to AI

• CHANCES* Consortium for Natural Hazards

• Taking the Chances out of AI

*Conveying Hazards And Catastrophes through Extracted Simulations

Like David Foster Wallace’s fish who had no clue what water was in spite of being immersed in it, many of us have a similar lack of awareness of being immersed in AI. And AI, in turn, is immersed in stochastic data, that is, uncertain data. But isn’t all data uncertain? Exactly. That’s my point. The discipline of probability management allows us to store this data and more importantly do math with it.

• AI is trained on Stochastic Data

• AI can output Stochastic Data if you have a place to store it and a way to use it.

• The Open SIPmath™ Standard offers both and is the only such standard of which I am aware.

My three videos stress that probability management is really about a new category of data, not new tools. I believe that data categories may be defined in terms of the operations which may be performed on it and the queries which may be made of it.

For example, Numeric Data may be operated on by the Arithmetic (accent on the third syllable when used in this context) operators +, -, * and /. The queries are >, < or = relative to some other piece of numeric data. Stochastic Data that obeys the principles of probability management may also be operated on with +, -, * and /, but instead of simple inequalities, it supports statistical queries such as the chance of a data element being greater or less than some target, or a percentile or statistical average.

As another example, Audio Data may be operated on with a mixer, to combine various tracks into a finished piece of music. The only query is Listen or not.

Speaking of Audio Data, my last album, which dropped in 1999, was called Exponential: Music from the Analog Age. For those who want to learn more, or execute the Listen query, read on.

Exponential Liner Notes

In the early 1970's after I had abandoned traditional Management Science, but before I had discovered spreadsheets, I tried unsuccessfully to be a folksinger in Chicago.

There were two things that dissuaded me from a career in music. First, there were a lot of people who were a lot better than I was, and second, they weren’t making it either. During this period, I did some recording on a Sony 4 track reel-to-reel tape deck with my stepbrother John Pearce (who is still an active musician).

I found the decades old tapes in my garage in 1999 and discovered to my amazement that there were still magnetic signals on them. All the recordings were between 15 and 20 years old at that time. Some pieces, like the patient who has been frozen in liquid nitrogen until a cure is found for his disease, awoke to a world in which they could be substantially improved. The tempo of the title track, Exponential, for example, was sped up digitally without changing the pitch. Click here to listen to the full album.

Sam Savage (left) and John Pearce in the early 1980s in Sun Valley, Idaho

Copyright © 2024 Sam L. Savage

Our History in the Journal of Portfolio Management

By Dr. Sam L. Savage 

The prestigious Journal of Portfolio Management has just published a special issue in memory of Harry Markowitz, and I was honored by an invitation to contribute. I invited my old friend Ben C. Ball as my co-author. Together we applied Harry’s modern portfolio theory to petroleum exploration, as described in Ch. 28 of my book The Flaw of Averages, and changed the trajectory of my career.

The JPM article, written as a docudrama, chronicles meeting Ben in the1980s, Harry in the 1990s, and developing an application that I dubbed the Markowitzatron in the 2000’s while consulting to Shell. The work at Shell was really the dawn of the discipline of Probability Management.

An on-line version of the article is available here. You need to enter your name and email to gain access, then search for “Markowitzatron” to be taken to the article.

Harry Markowitz, 1927-2023

Sam Savage

Ben C. Ball

Copyright © 2024 Sam L. Savage